Collection Home
Here I discuss interpreting pull-testing results to determine equipment strength. This page uses simulated data to illustrate some very common errors people make when interpreting results[1].
Let us pretend that I want to find the breaking strength of Fictitious ascenders[2]. Let us assume that their average breaking strength really is 5000 pounds (22 kN) and that manufacturing variations really have a standard deviation[3] of 200 pounds (1 kN). Pull-testing some of these should tell us something[4]. Breaking only one will not tell us much[5], so we will need to break more than one.
Here is my example:
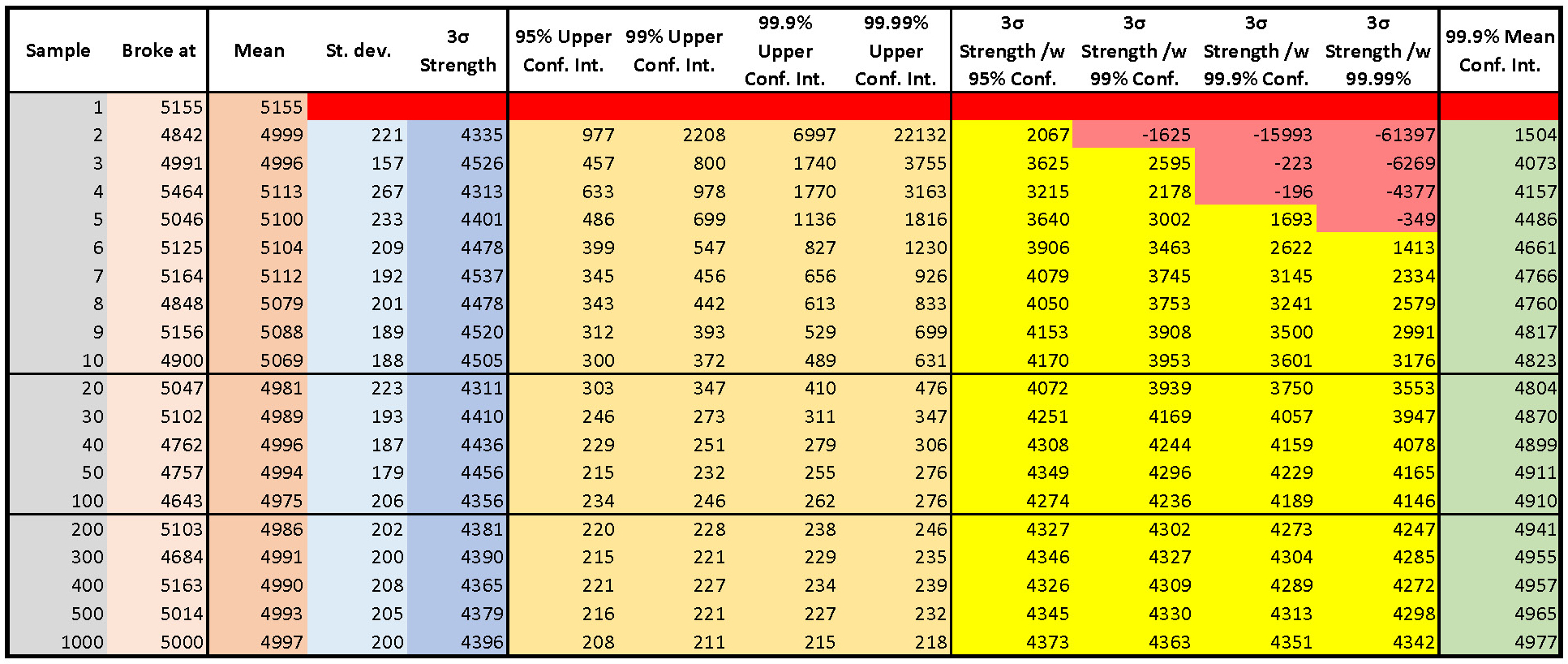
Let us look at the table. The "Broke at" (tan) column shows simulated test results for 1000 tests (I hid most of the rows to save space). I calculated these using the ridiculous[6] but useful assumption that the real breaking strengths were normally distributed.
The brown "Mean" column averages all the results down to that sample[7]. Notice that the numbers in this column bounce[8] around as we perform more tests, but eventually the mean starts to get close to the "real" ("correct") value. In this example, it took 11 samples before the mean settled to within 1% of the true value[9].
The light blue "Std. Dev." column reports the standard deviation of all samples up to that row. There is no value in the first row because we cannot estimate variation with only one sample. Once again, the numbers bounced around as we tested more samples. They did not settle to within 10% of the true value until sample 53 and to within 1% until sample 644[10].
Some manufacturers have standardized on reporting "3σ" strength. They argue that only 1 in 1000[11] samples will break at more than 3 standard deviations from the mean. This is not true[12]. They estimate the "3σ" strength by taking their sample mean and subtracting three times their sample standard deviation. The darker blue "3σ Strength" column calculates these values for our tests. How good is this calculation?
Let us look at the row for 10 samples. The standard deviation of the first ten tests is 188. Now look at the four gold columns labeled with "Upper Conf. Int." From left to right, assuming the "real" samples came from a normal population[13], we can be 95% sure that the true standard deviation is less than 300, 99% sure for less than 372, 99.9% sure for 489 and 99.99% for less than 631. Most statisticians would choose 95% or 99% (or even 90%), but you can choose for yourself[14].
The four yellow columns calculate the "3σ" strength calculated using the limiting standard deviations in the four yellow columns. As you can see, testing a small number of samples does not give useful results if we insist on being confident in the conclusions that we draw from our data. We need to break a lot of Fictitious ascenders to have justified confidence in our results.
So far, we have been using the test results to estimate the average breaking strength and its standard deviation, and to see how confident we can be with our results.Let us now focus on simpler and perhaps better question: how much confidence can I have in the average breaking strength calculated from my test results? This is in the gray column at the right.
For simplicity, I only indicated the case where I wanted 99.9% confidence. Look at the entry in the second row, which is based on only breaking two samples. It means that we can be 99.9% confident that the actual breaking strength is 1504 pounds, and that there is a 1 in 1000 chance that it is less than 1504 pounds. Based on the test data only, we expect a 1 in 1000 chance that half the Fictitious ascenders will fail at less than 1505 pounds.
Let that last sentence sink in. Discouraging, to say the least. Why is this number so low? We wanted to be very confident (99.9%) that the actual average breaking strength was higher than the number we calculate in this column[15], but testing only two Fictitious Ascenders cannot provide much confidence. If you want results that you can trust, you need to have a lot of results. As we test more ascenders, we start to get more reasonable numbers in which we can have such high confidence. The ridiculous assumption that breaking strength has a normal distribution also contributed[16].
[1] I have taken multiple undergraduate, graduate, and industry courses in statistics totaling over 300 hours, applied them extensively in my professional career, and have taught the subject. I am no expert by any means, but I have learned to be careful.
[2] This is different from finding out how safe it is. There is more to safety than just strength.
[3] A common and specific calculated result that describes the extent of the variation.
[4] The only “right” approach is to pull test every single one and then look for the lowest result. That would be impractical, expensive, and would not leave any for us to use. That may explain why nobody has a Fictitious Ascender.
[5] We have no idea whether this result is typical or an extremely rare event. The ONLY think that one test result tells us is that sample broke at a particular value. Any other conclusion requires an assumption, which is the same thing as assuming our conclusion.
[6] Assuming a normal distribution means assuming some samples will have negative breaking strengths and that some could be arbitrarily large. Both are physically untenable. Despite this, most results will be near the mean and so the assumption is useful. Besides, this is not this column that really interests us.
[7] e.g., the value in the mean column opposite sample 4 is the average (mean) of the results for samples 1, 2, 3, and 4.
[8] In a perfect world, these would all be 5000. The world is not perfect.
[9] Depending on how nit-picky you are. If we repeat the process with a different 1000 tests, it will take a different but hopefully similar number of tests before the results settle out to “close enough.”
[10] Getting a good sample standard deviation takes a lot more testing than getting a good sample mean.
[11] This is 1 in 741 rounded off to make it sound better. If you assume a symmetric distribution and only count low vales, you can argue it is 1 in 1482.
[12] They assume that the breaking strength follows a normal distribution, which is physically absurd. It is a reasonable approximation for many other distributions if you stay near the mean, but tends to underestimate the probability for many real-world distributions as you move farther from the mean.
[13] Never true, but sometimes a useful approximation.
[14] It is only your life.
[15] Lower confidence yields a higher calculated number, but increases the chance that the correct average breaking strength is lower than the number that you will be betting your life on. What is your life worth?
[16] Remember, assuming a distribution amounts to the same thing as assuming the answer.
[17] Do not think that you need to have high breaking strengths to allow for a large safety factor. Most accepted “safety factors” are arbitrary numbers that are low enough that making them smaller does not save much money and high enough that not enough people have died. In either case, they work. If you know how to select safety factors based on statistical data, you will understand my pervious sentence.